At the beginning of each month a Math challenge will come out.
To solve the challenge correctly, you have to:
- Write the solution with an explanation on a paper with your name and group and left it in the mailbox situated in the hall, before the first day of the following month.
- Write the reasoned solution in this website (at the bottom of the article).
There will be 3 categories:
- Pupils (ESO, Batxillerat and Professional Studies).
- Teachers and PAS.
- Web visitors.
We drew and coloured six figures, each one in square papers of the same size. How many of these figures have the same perimeter as the paper?
February Challenge
For ESO students: We drew and coloured six figures, each one in square papers of the same size. How many of these figures have the same perimeter as the paper?
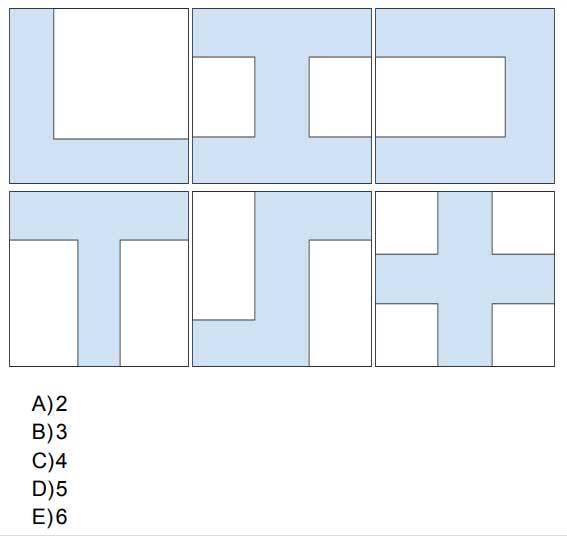
And for the rest of pupils:
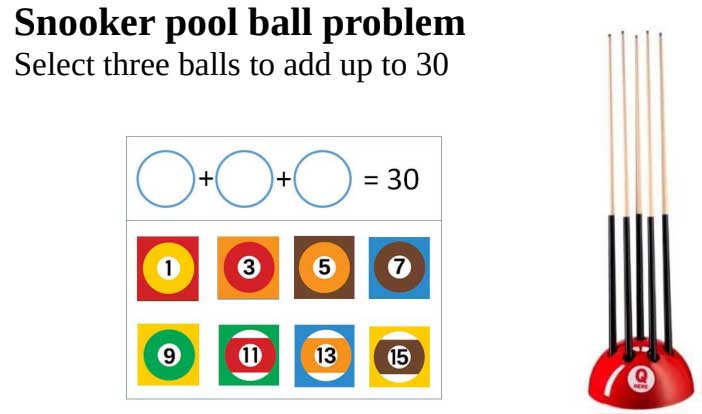
January Challenge
Chester’s High School has organized a chess tournament and Berta has signed up. Each player will play a game against each of the other contestants, except, obviously, against himself. The winner of the game scores a point. If the result is a draw, each player scores half a point. At the end of the tournament it turns out that, excluding Berta, the rest of the players scored a total of 99 points. How many players had signed up for the tournament? How many points did Berta get?
*Solution

December Challenge
For ESO pupils:

*Solutions (pddf)
Correct answers: Nuria B. (teachers), Maya Treuvat (1BACT), Maria L. (4.2 ESO), Pau R. (1BACT), Subaru B. (1BC) and Martí D. (1BC)
November Challenge
Correct answers: Nuria B. (teachers), Maya Treuvat (1st Bat CT).
For ESO pupils:
After Halloween, it’s time for a new math challenge! In this month’s challenge, you
have to look closely at these sums. They seem wrong, but that’s because they are
not ordinary sums. I encourage you to try to find the pattern. Once you figure that
out, what will be the result of the last operation?
For everybody else:
We write a long number putting consecutively: 2003, 2004, 2005,…: 20032004200520062007…
Which digit is in 2004 position?
Solution:
2004: 4 = 501 grups de 4 dígids
2003 + 500 = 2503 per tant a la posició 2004 hi ha un 3
October Challenge
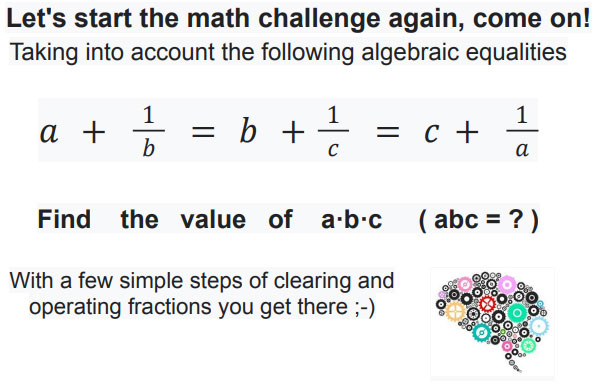
Correct answers: Nuria B. (teachers), Maya Treuvat (1st Bat CT) and Anonymous (talk to your MAT teacher).


