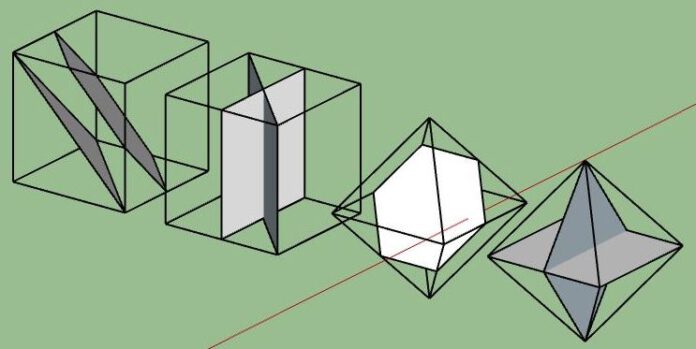
Un cop acabat l’aprenentatge de les operacions dièdriques a Dibuix Tècnic, hem plantejat a l’alumnat introduir el tema de poliedres regulars dibuixant directament amb el programa Sketch Up. En només una sessió han pogut dibuixar 3 dels poliedres i a més de manera orgànica hem localitzat la majoria de seccions importants d’aquestes figures màgiques.
Podeu descarregar l’arxiu amb els poliedres per treballar amb el programa SketchUp amb els vostres alumnes.
Dibuixar aquestes seccions és una bona activitat per desenvolupar habilitats geomètriques. Es tracta de figures que han obsessionat durant mil.lenis artistes, arquitectes i matemàtics.
Per fer-ho cal dibuixar inicialment sobre un pla dos cares desenvolupades per després re-abatre una d’elles: apliquem de manera intuitiva allò après anteriorment en sistema dièdric.
HEXAEDRE. Quadrat, rectangle, triangle equilàter, hexàgon regular i rombe.
Detall de les seccions del triangle equilàter i hexàgon regular.
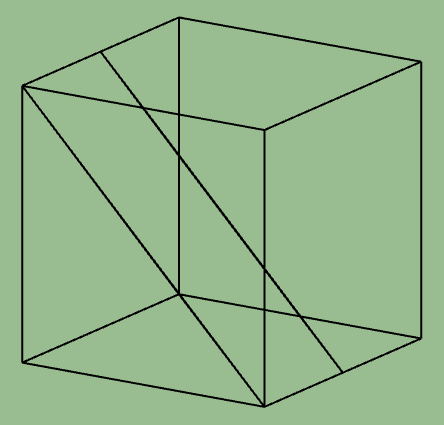
TETRAEDRE. Quadrat, triangle isòsceles i triangle equilàter.
OCTAEDRE. Quadrat, rombe i hexàgon regular.
A la segona sessió de treball l’alumnat ha copiat els models creats i ha dibuixat els seus conjugats.
POLIEDRES CONJUGATS. Es tracta d’un poliedre inscrit en un altre: aquesta situació es dóna quan el nombre de cares d’un poliedre coincideix amb el nombre de vèrtex d’altre i viceversa. L’octaedre i el cub ho son entre sí. També l’icosaedre i el dodecaedre. El tetraedre ho és en relació a sí mateix. Per fer-ho només ha calgut la localització de l’incentre de cada cara.
A partir d’aquí podem utilitzar aquests models per estudiar casos d’interseccions i distàncies en verdadera magnitud. L’alumnat amb dificultats pot fàcilment establir relacions entre el que es demana a partir del gir i l’estudi dels poliedres creats. També pot ser útil plantejar a l’alumnat la creació d’enunciats relacionats amb aquestes figures.